Given the option, would you take $100 today or $100 in 1 year? I’m guessing you said you’d take the money today, which means you’re already following the tenants of the time value of money. The idea of the time value of money is that money received today is “worth more” than money received at a future date… and here’s why:
| Balance if money is received today | Balance if money is received 1 year from today | |
| Today | $100.00 | $0.00 |
| 1 Year from Today | $105.00 | $100.00 |
The example above assumes that if you receive the money today, it is invested in an account that earns interest at a rate of 5% annually. Now, a 5% interest rate could be whatever amount is appropriate based on how that money is working for you. It could be in a savings account, a money market account, in the stock market, and so on, all of which will have different interest rates.
Compound Interest
Another important concept when discussing the time value of money is compound interest. The interest in the example above is compounded annually, but interest can compound at any rate: semi-annually, quarterly, monthly, daily, even continuously. If the $100 was compounded semi-annually, it would be worth $105.06 at the end of the year. The extra $0.06 comes from the fact that the principal balance is greater than $100 after the first compounding period.
Compounding Period 1: $100.00 x 2.5% = $102.50
Compounding Period 2: $102.50 x 2.5% = $105.06
In the above equations, the first value is the principal. So the principal for the initial compounding period is $100.00, but for the second, the principal becomes the total value after the first compounding period, so $102.50. It is also important to note that when the compounding period is more frequently than annually, the annual interest rate must be reduced accordingly. So, for this example, interest compounds 2 times per year, so the interest rate for each compounding period is the annual interest rate divided by 2, or 5% / 2 = 2.5%.
When you’re talking about semi-annual compounding on a $100 balance, you get an extra $0.06, but let’s see what it looks like if we have more compounding periods:
| Compounding Periods | End of Year Balance |
| Annual | $105.00 |
| Semi-Annual | $105.06 |
| Quarterly | $105.09 |
| Monthly | $105.12 |
| Daily | $105.13 |
So, as you can see, the more compounding periods per year, the more you earn in interest, which is “extra” money for you!
Talking about $100 over one year period is a good example, but lets look at some larger amounts over longer periods of time that would be more representative of, say, retirement savings.
Retirement Savings
Let’s make the following assumptions:
- Retirement Age: 67
- Monthly Contributions: $100
- Annual Return: 7% (NOTE: Stocks will go up and down over time, but the average stock market historically has been approximately 7% when adjusted for inflation)
- Compounding: Monthly
The graph below shows what the total account balance would be at retirement age based on a different starting age of savings. The graph also shows the split of contributions versus interest based on these assumptions.
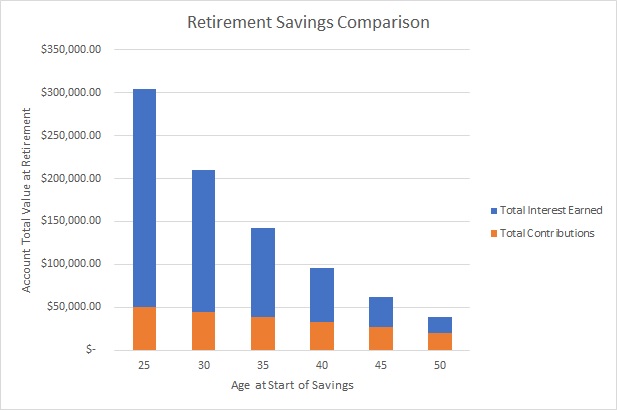
As you can see, the earlier you start saving, the more you contribute, but earlier savings also gives you more time to earn interest, which can be substantial, particularly over a long period of time. If you’re not a numbers person, feel free to skip ahead to the next paragraph, but if you’re interested in the numbers used to build this graph, let’s take a look:
| Age at Start of Savings | Years of Savings | Total Contributions | Contributions Percent of Total | Total Interest Earned | Interest Percent of Total | Total Value of Account |
| 25 | 42 | $50,400.00 | 17% | $253,970.73 | 83% | $304,370.73 |
| 30 | 37 | $44,400,00 | 21% | $165,254.44 | 79% | $209,654.44 |
| 35 | 32 | $38,400.00 | 27% | $104,441.10 | 73% | $142,841.10 |
| 40 | 27 | $32,400.00 | 34% | $63,310.63 | 66% | $95,710.63 |
| 45 | 22 | $26,400.00 | 42% | $36,064.56 | 58% | $62,464.56 |
| 50 | 17 | $20,400.00 | 52% | $18,612.62 | 48% | $39,012.62 |
In this case, we’re assuming the savings occurs monthly, but the starting point is different. This means that for those who start saving earlier, their total contributions will be greater. However, you can see from the graph and table above, that the earlier the savings begins, the higher the percentage of the total comes from interest. This is a function of the time value of money!
So what does all this mean? The sooner you start saving and the longer you can let your savings grow, the more money you will have contributed toward your goal, but you’ll also have earned more interest! So, let’s get saving!
